As you play Match Poker Online™, you’ll see certain symbols and numbers appearing together.
A key feature of Match Poker Online™ is that we, highly accurately, determine the better poker players.
We then show you where you rank with your IFMP Rating.
Your IFMP Rating does not work like ‘Experience Points/XP’ in other games. Experience Points are almost always awarded regardless of your performance; those who play most will have the most. Your rating, on the other hand, are solely a reflection of your skill.
As your IFMP Rating increases, your symbol will change, showing where you rank within the 49 different ranking groups. (Here, every 200 points confers a new colour, broken down into the four suits) – so increasing your IFMP Rating by 50 means you progress to the next symbol – such as below.
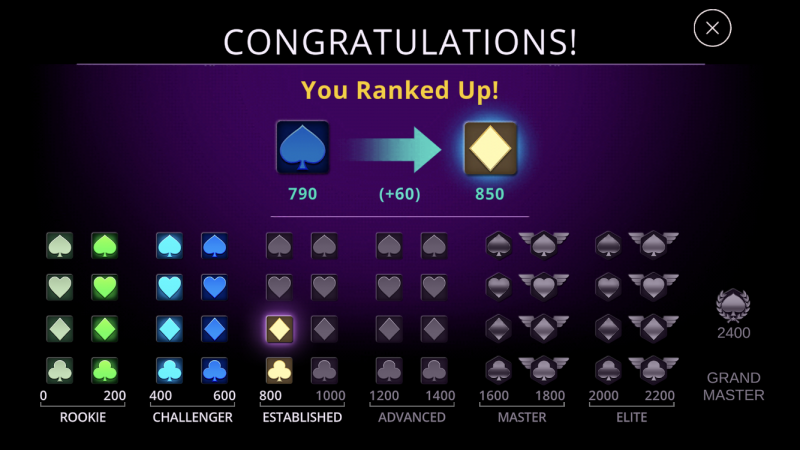
What does my IFMP Rating mean?
The International Federation of Match Poker is the governing body of sports poker, promoting poker and its Match Poker™ variation as a skill game and a mind sport. The IFMP is to Match Poker what the ICC is to cricket, or what the FIA is to Formula One.
The IFMP is approved by the Global Association of International Sporting Federations (GAISF), which works closely with the International Olympic Committee. Learn more about the IFMP here.
The IFMP endorses the Ratings that the Match Poker Online app confers on players, making them official and global.
The app uses a highly sophisticated rating system in which your IFMP Rating represents the likelihood that you will beat other players. If two players have the same Rating, it means they have an equal chance of beating each other. If one player has a higher Rating, they are more likely to win.
To assure the accuracy of our Leaderboards, and ensure more competitive games, we use your Rating to matchmake you against players of similar skill levels.
Please note, however, that until you have played 30 matches, your Rating will carry a ![]() symbol. This indicates that this is a Provisional Rating only – and becomes a full, accurate rating, by the time you have played 30 matches. This is explained in more detail in Part 3 of 3.
symbol. This indicates that this is a Provisional Rating only – and becomes a full, accurate rating, by the time you have played 30 matches. This is explained in more detail in Part 3 of 3.
Part 1 of 3: How and why does a player’s IFMP Rating change?
All players start with an IFMP Rating of 0.
We then use our own custom modification of a sophisticated algorithm known as ‘OpenSkill’ to determine changes in your Rating after every match.
[OpenSkill is an open-source library that is an implementation of the public domain Weng-Lin algorithm. It’s comparable in accuracy to Microsoft’s TrueSkill algorithm, but up to 20 times faster, so we can more accurately rank tournaments with hundreds or thousands of players.]
You may be familiar with the Elo Ranking System, used in chess; OpenSkill is like that but on steroids.
While the algorithm is a complicated beast, the theory is simple. Your change in Rating at the end of the match is dependent upon three things:
- What is your pre-match Rating?
- What are the pre-match Ratings of your opponents?
- How does your final score in the match compare to your opponents’?
Because an IFMP Rating is an ‘expectation’ of how likely it is that you will beat someone, your Rating will only change if your result doesn’t fit those expectations. Some examples:
Example 1: Two players have vastly different Ratings:
Let’s say you have a Rating of 800 and Joanna has a Rating of 2200. The algorithm therefore expects Joanna to win. If Joanna does indeed win, the algorithm has no reason to change its expectation, so it is likely that neither player’s Rating would change.
Example 2: Two players have a similar IFMP Rating:
Let’s say you and Bob both have a Rating of 1239. OpenSkill therefore predicts a tie between you. If one of you wins, the algorithm will have to change its expectation. It does this by adjusting the Rating of both players, e.g. Bob’s Rating will go up and your Rating will go down if Bob wins. If Bob were to win again and again, the gap between your Ratings would increase.
Example 3: There is an ‘upset’ result:
Let’s say you have a Rating of 900 and you beat Aarav who has a Rating of 1400. The algorithm now realises that its expectations about your relative skill levels were wrong, so it will raise your Rating and reduce Aarav’s.
This is also how Elo works but, in Match Poker Online, you could be competing against not just one but many opponents.
Working out how every player’s Rating ought to change can become very complicated, especially when eight players’ results do not conform to the order of their Ratings, for example:
| Placing at end of match | Player Name | Pre-Game Rating |
|---|---|---|
| 1st | ChallengerGuy | 707 |
| 2nd | AdvancedGirl | 1390 |
| 3rd | RookieBoy | 397 |
| 4th | EstablishedPerson | 821 |
| 5th | MasterLady | 1945 |
| 6th | EliteMate | 2300 |
| 7th | RookiePlayer | 103 |
| 8th | ChallengerDude | 468 |
Look at EstablishedPerson (in fourth place). This player beat 2 players rated lower (as expected), beat an Elite player and a Master player (unexpected good results) BUT also lost to a Rookie and a Challenger (unexpected bad results). So… what happens?
This is why we use the OpenSkill algorithm.
Part 2 of 3: What is skill and how does an IFMP Rating capture it?
‘Skill’ is not a single number!
While we represent skill as a single number (i.e., your Rating), it is, in fact, a range. Specifically, skill is a range of probabilities around an average or mean. The probability is greatest that a player will perform very close to their mean and becomes less likely as you move further away from that point.
If you are playing tennis against World No. 1, Novak Djokovic, you are expected to lose. But, if you play him a million times, you might win one or more times (he might be ill or have an injury). As the best in the world, Djokovic’s mean is higher than everyone else’s, but the probability that he will lose to you is not zero, it’s just very low.
So, a player’s skill can be accurately represented by a bell-curve (specifically, a Gaussian Distribution), as below:
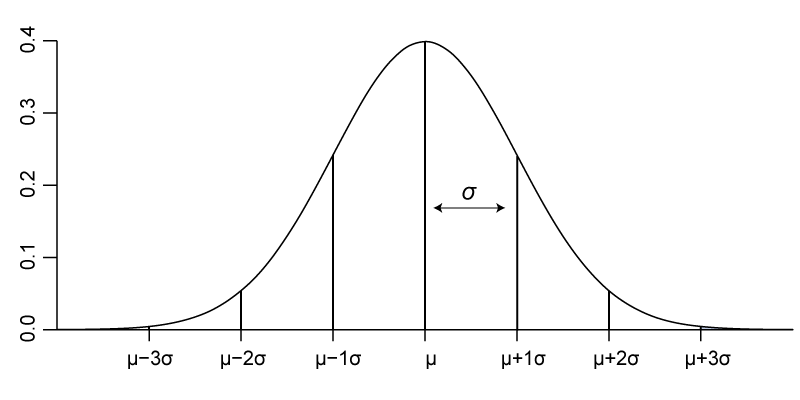
The y-axis of this graph indicates the probability that a player will perform at a given level. Their average or ‘mean’ skill value is denoted by the Greek letter ‘mu’ (µ). This represents the level of skill (shown on the x-axis) at which the player is most likely to perform.
But the OpenSkill algorithm uses two key factors to reach the single number that we use to represent players’ skill levels. The second factor, represented by the Greek letter ‘sigma’ (σ), is the player’s Standard Deviation1. This reflects the degree of uncertainty of a player’s performance and determines how wide or tight the curve is. When the algorithm has lots of information about how a player has performed, the curve will be quite tight – reflecting a higher degree of confidence as to their skill level. If the algorithm does not have much information (or the player plays very inconsistently), the curve will be quite wide.
In summary, σ represents the uncertainty surrounding a player’s expected performance, while µ represents the player’s average (and therefore most expected) performance.
Our algorithm starts with no information about how skilled a player is, so all players start with a µ of 1200, exactly halfway between 0 and 2400 – i.e. dead average.
With no information, there is total uncertainty (i.e., no degree of confidence) around this estimate, and so all players start with a σ value of 400, which is extremely high. This sigma value decreases as the player plays more matches and the algorithm obtains more information about their skill.
Mu and sigma form the basis of how we calculate changes in players’ Ratings. After every game, these two values change. We then use a simple formula to convert them into the single number that denotes your Rating.
“Rating Decay”
The term ‘Rating Decay’ is a consequence of the way the algorithm works.
If a player has not played any games of Match Poker in a while, the algorithm grows more uncertain in that player’s skill. Uncertainty in a player’s skill is captured by σ, so a player’s σ increases if they have not played a match in a while. As you’ll see in part 3 (below), the consequence of an increase in σ is that it decreases a player’s Rating.
Therefore, players can expect their IFMP Rating to fall by a small amount if they do not play for a while, although this decay is limited (and certainly not perpetual). A player’s Rating can only decay due to inactivity as long as their σ is lower than its starting value. A player’s µ, on the other hand, never changes due to inactivity.
Part 3 of 3: How is your actual ‘IFMP Rating’ number calculated?
We convert your mu and sigma to our ordinal Rating number using this formula:
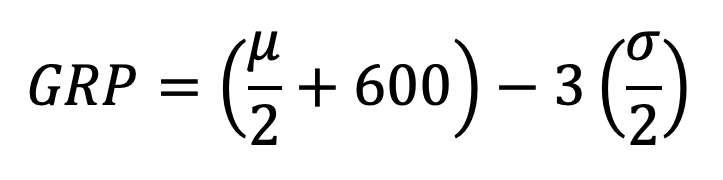
However, we tweak this number further. Our surveys showed that:
- Players did not like seeing wild fluctuations in their Rating as the algorithm sought to get a handle on how skilled they were.
- Players preferred to see their progression through the ranks as linear. This increases their confidence and allows them to see their trajectory throughout their experience in Match Poker.
- Below-average players did not enjoy starting the game at a Rating of 1200 and frequently seeing negative changes to their Rating.
So, the formula above only applies after a player has played 30 Battle Royale matches (or equivalent) in Match Poker Online (note: one match of Battle Royale equates to 32 hands of Quick Play).
Before this point, we apply a logarithmic growth function to a player’s Rating. This is why players’ Ratings are provisional ![]() until they have played 30 matches. After this point, we are confident that the algorithm has enough information about a player that their Rating accurately reflects their true skill at Match Poker, and they will have made their way from a Rating of 0 to their true Rating smoothly over their first 30 matches.
until they have played 30 matches. After this point, we are confident that the algorithm has enough information about a player that their Rating accurately reflects their true skill at Match Poker, and they will have made their way from a Rating of 0 to their true Rating smoothly over their first 30 matches.
Footnotes
1. The likelihood that a player performs within one Standard Deviation (µ ± 1σ) of their Mean is about 68%. It is 95% likely they will perform within two Standard Deviations of their Mean (µ ± 2σ) and 99.7% likely they will perform within three Standard Deviations of their Mean (µ ± 3σ).
